Have you ever checked the Rotten Tomato score of a movie before deciding to watch it? And then which one do you check–the critic or audience score? Will either matter in your enjoyment of the movie? I’ve decided to take a stab at answering these questions by examining the 2022 movie ratings of three roommates (one of them being my wife’s sister, hence my access (with permission) to their scores). These are three professional women in their twenties living in Provo, Utah. I’ll refer to them as F, N, and A. This year they have watched twenty-five films so far, and you can see their self-rated levels of enjoyment (out of 10) of each film and the Rotten Tomato Critic score (rescaled to 10) below. You can click on the image to make it larger.

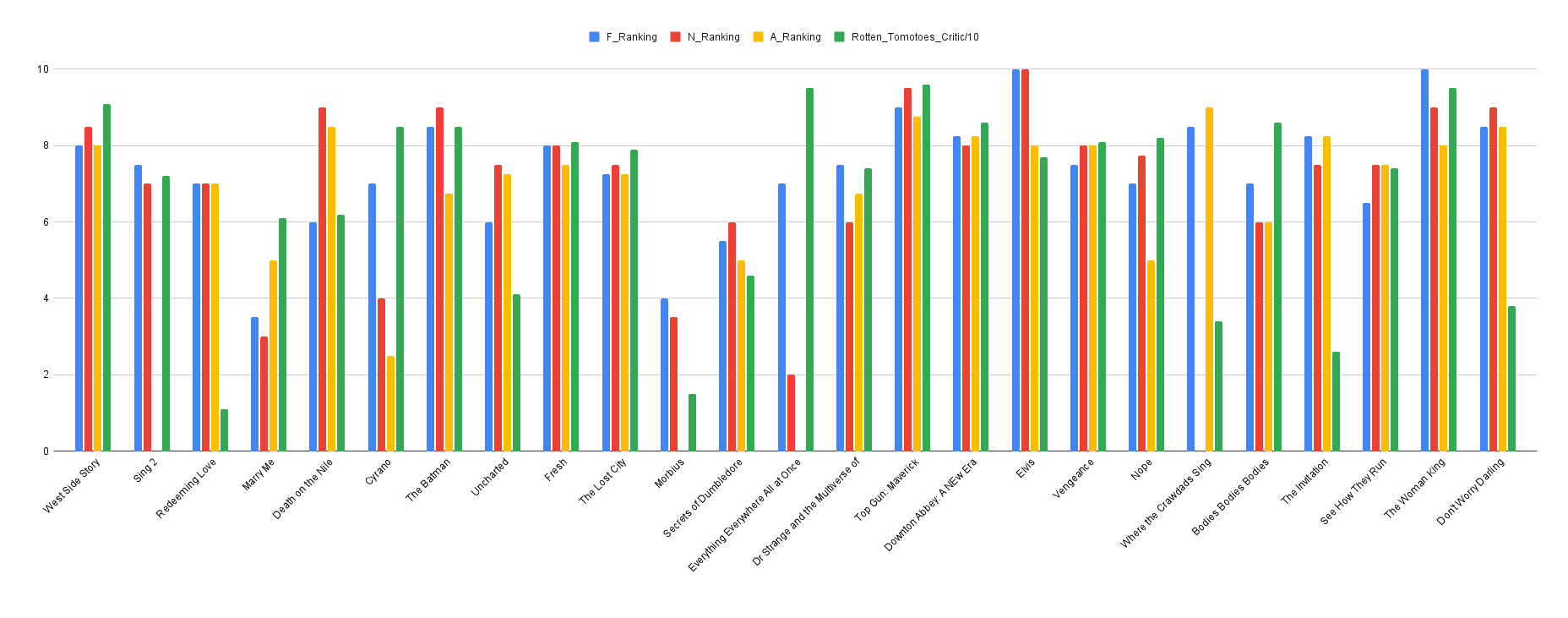
It is hard to visualize for each movie, so let’s average their ratings, and throw in the Rotten Tomatoes audience score too: 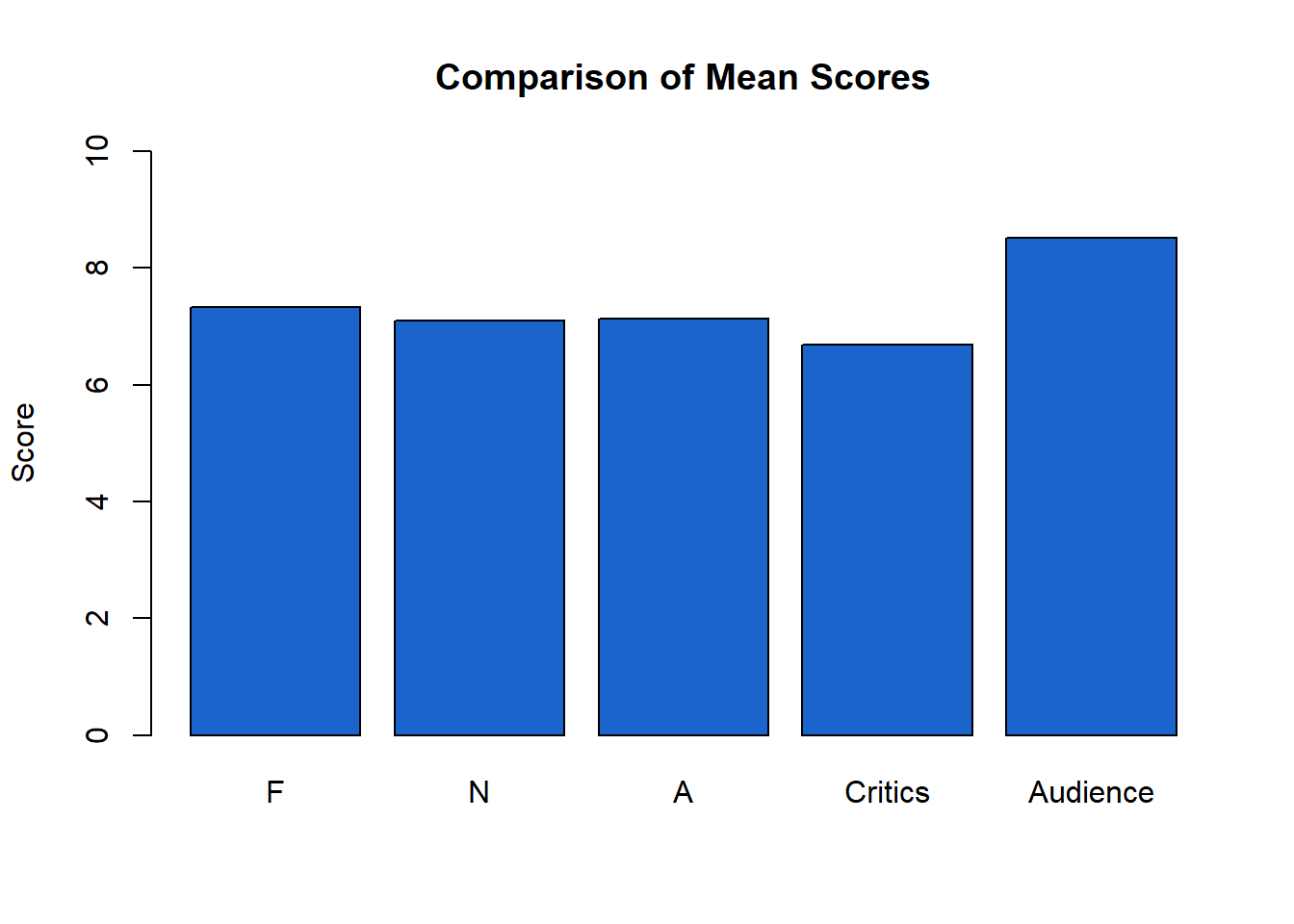And check out their distributions:

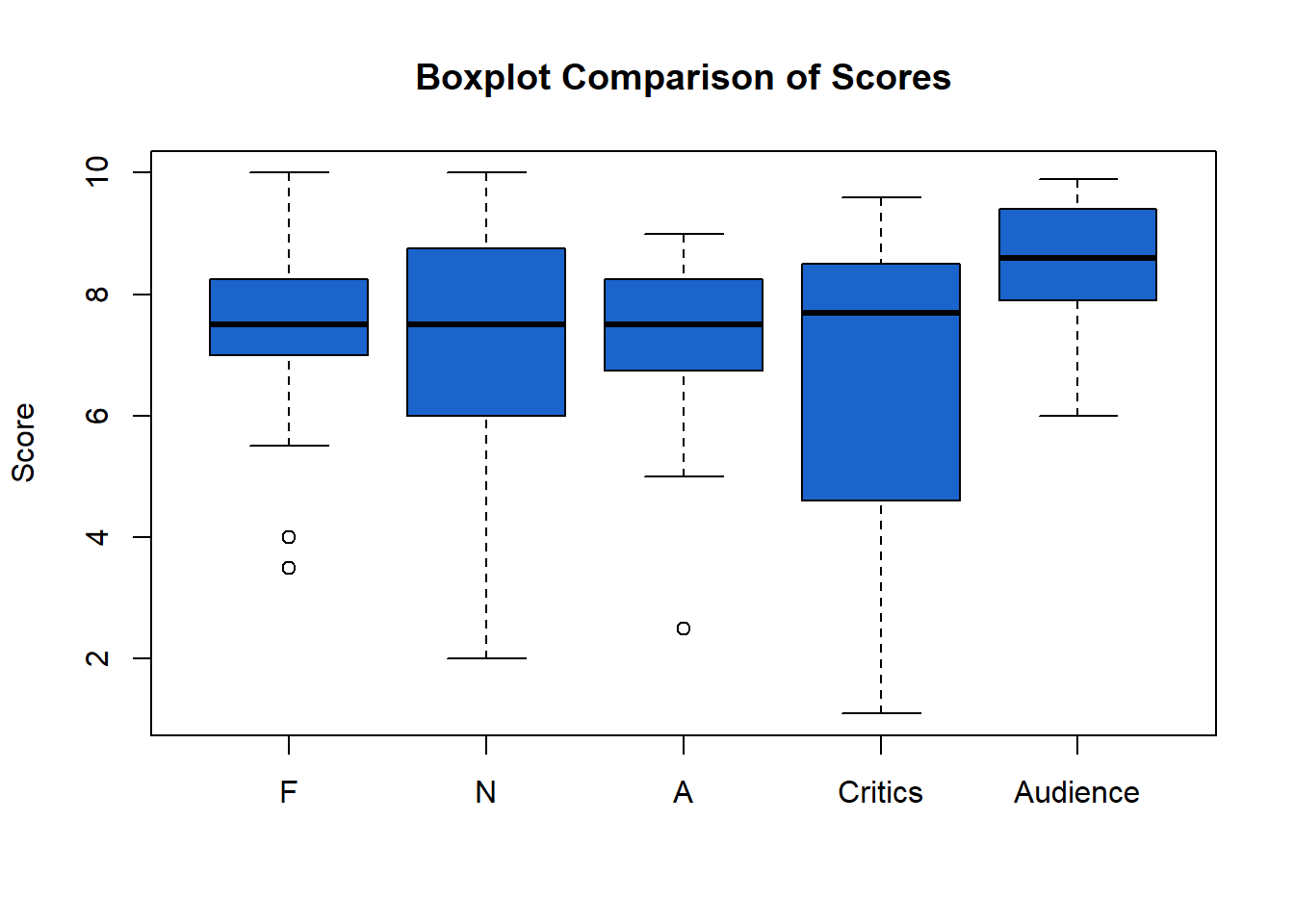If you’re unfamiliar with boxplot charts, see this handy guide. In short form, though, it’s just an easy way to visualize data dispersion. The taller the boxes, the more dispersed the observations. From both of the above graphics, you can see that the averages (whether measured by mean or median) between the three roommates are very similar; they have highly comparable reactions to these movies on average, which is probably a good thing for roommate relations. It’s funner to watch movies with people who share your tastes. N is a bit of a wild card though; she is both more positive and negative about the films they watch. She has the greatest range of reactions, despite landing on the same median score as her roommates.

Interestingly, the roommates tend to be nearly as critical of movies as the critics on Rotten Tomatoes, it is again just a question of range.¹ General audiences, however, tended to be much more enthusiastic about these movies when compared to the roommates.Makes sense–most people prefer going to watch movies they know they’ll enjoy.

Now let’s consider the relationship between the critics’ score and the enjoyment levels of each of the roommates.

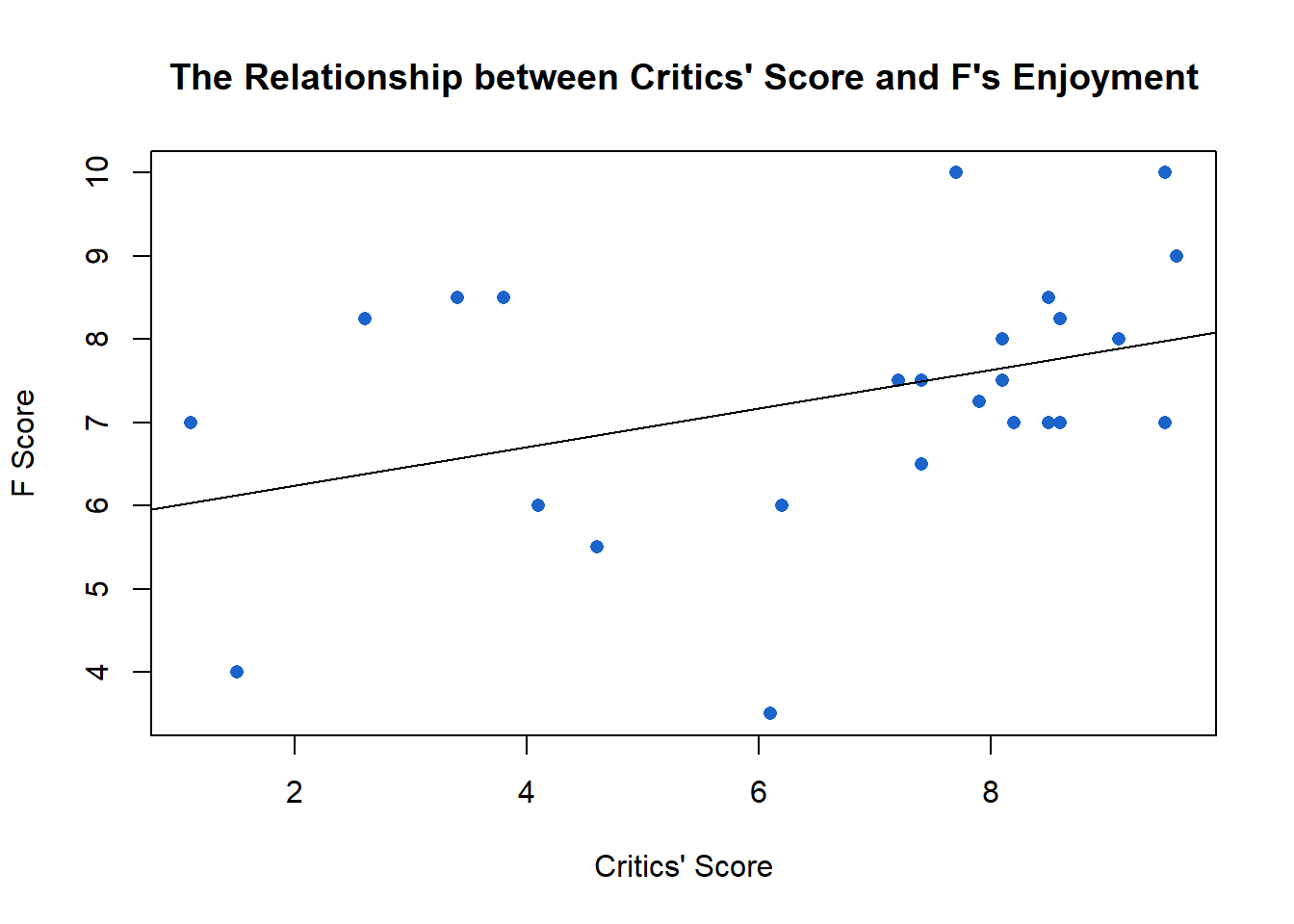
F’s enjoyment is modestly correlated with the critics’ score.² A one unit increase in the critics’ score for a movie is associated with a 0.23 increase in F’s enjoyment score. Using the original units, this would mean that when comparing two movies, where 80% of critics enjoy the one, and 90% of critics enjoy the other, F will enjoy the latter by about two and a half percentage points. Not a huge change unless you’re comparing two movies with Rotten Tomato scores of, let’s say, 20% and 90%. F should enjoy that movie about 16 percentage points more.

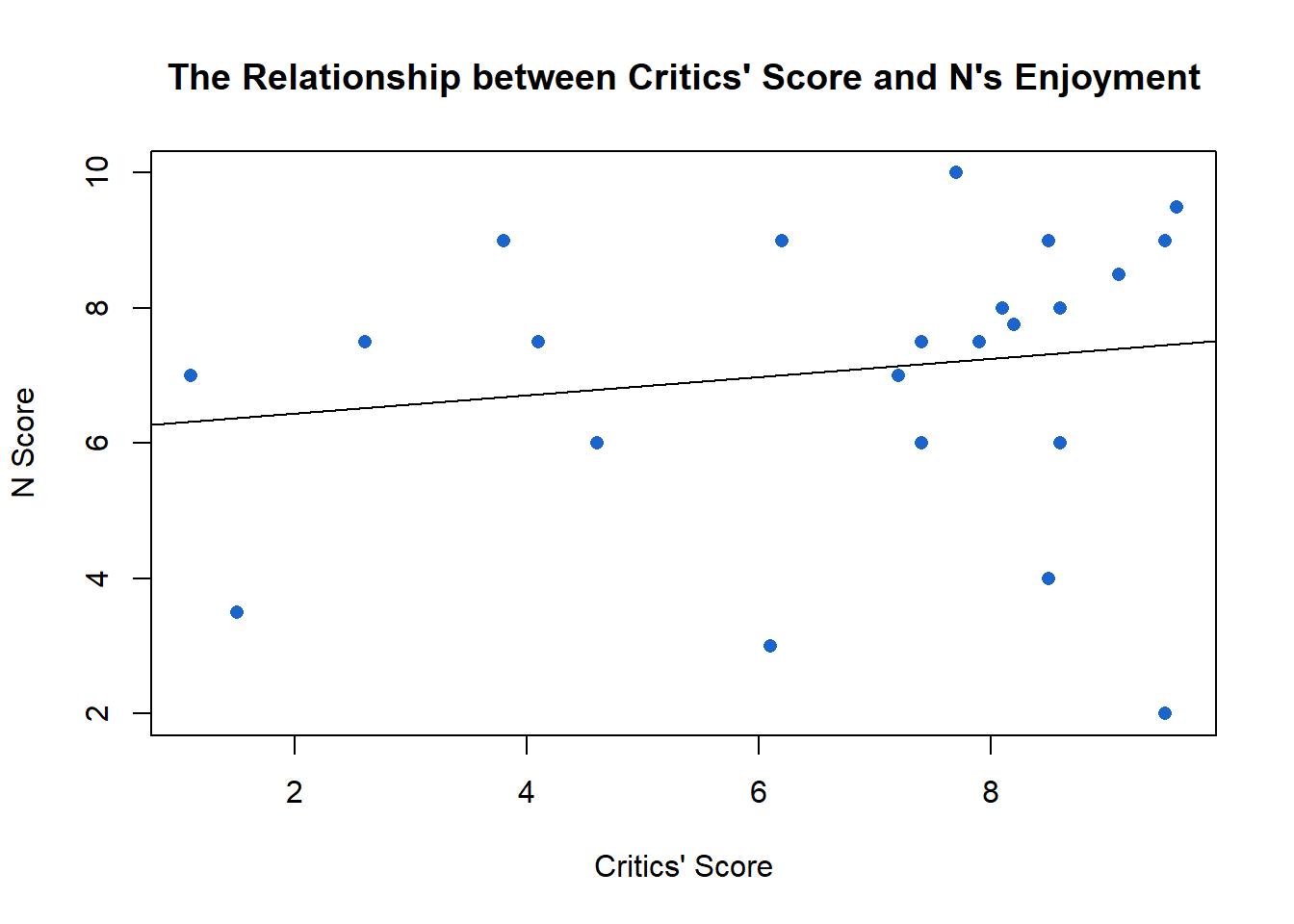
Similar but weaker for N.³ For her, a unit change for the critics is only associated with a 0.14 change for N’s enjoyment score.

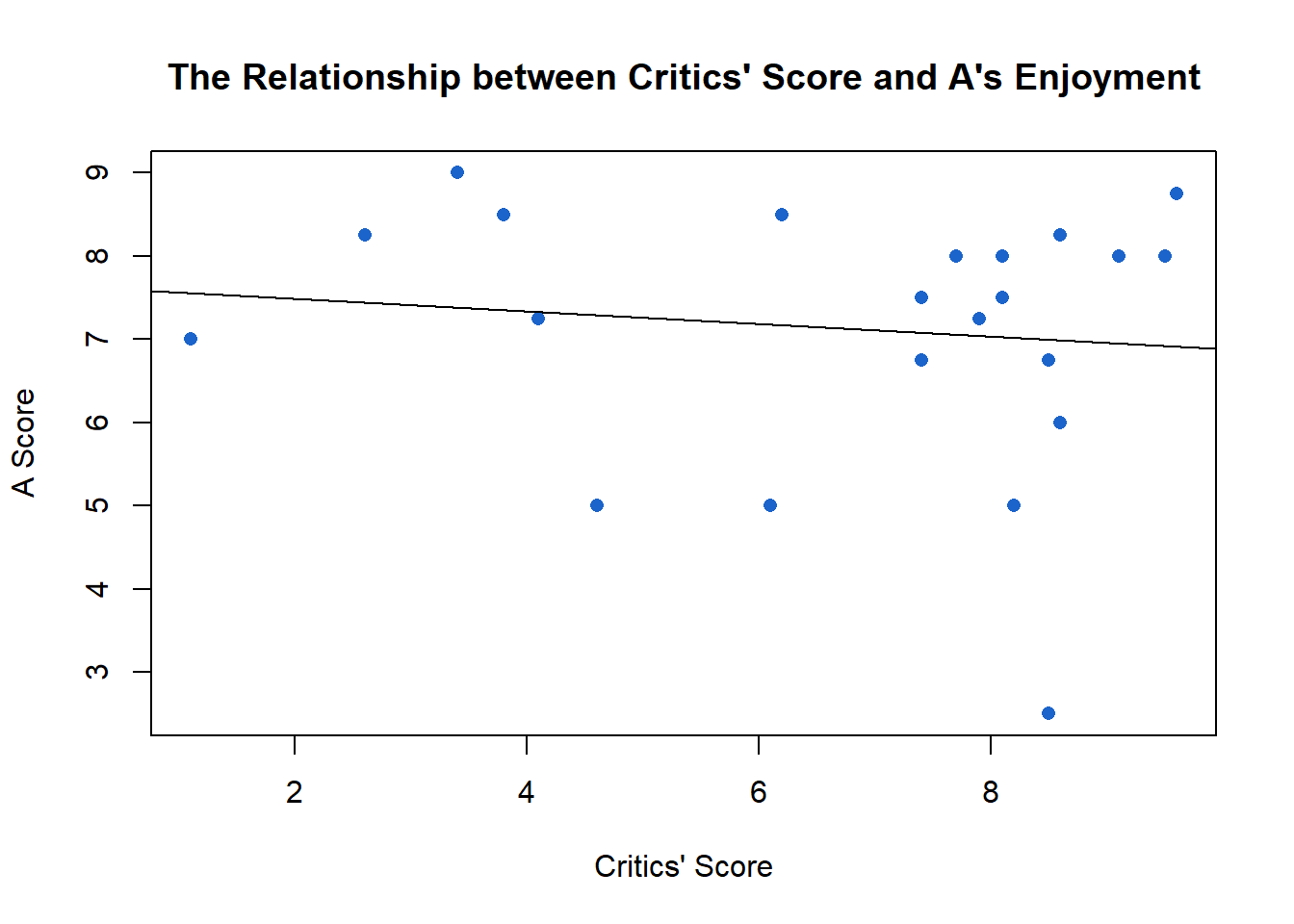
And A’s scores show an even weaker correlation with the critics’ scores.⁴ Notice how flat the regression line is, which predicts the relationship. Each observation is far from that line, meaning there is essentially no meaningful relationship. And even if there were a relationship, it would be (slightly) negative. We can also think about the total variation in A’s enjoyment as predicted by critics’ scores; it accounts for about 1% of the variation. This suggests that A should never worry about what the critics think about a movie.

What about the Rotten Tomato audience scores though?

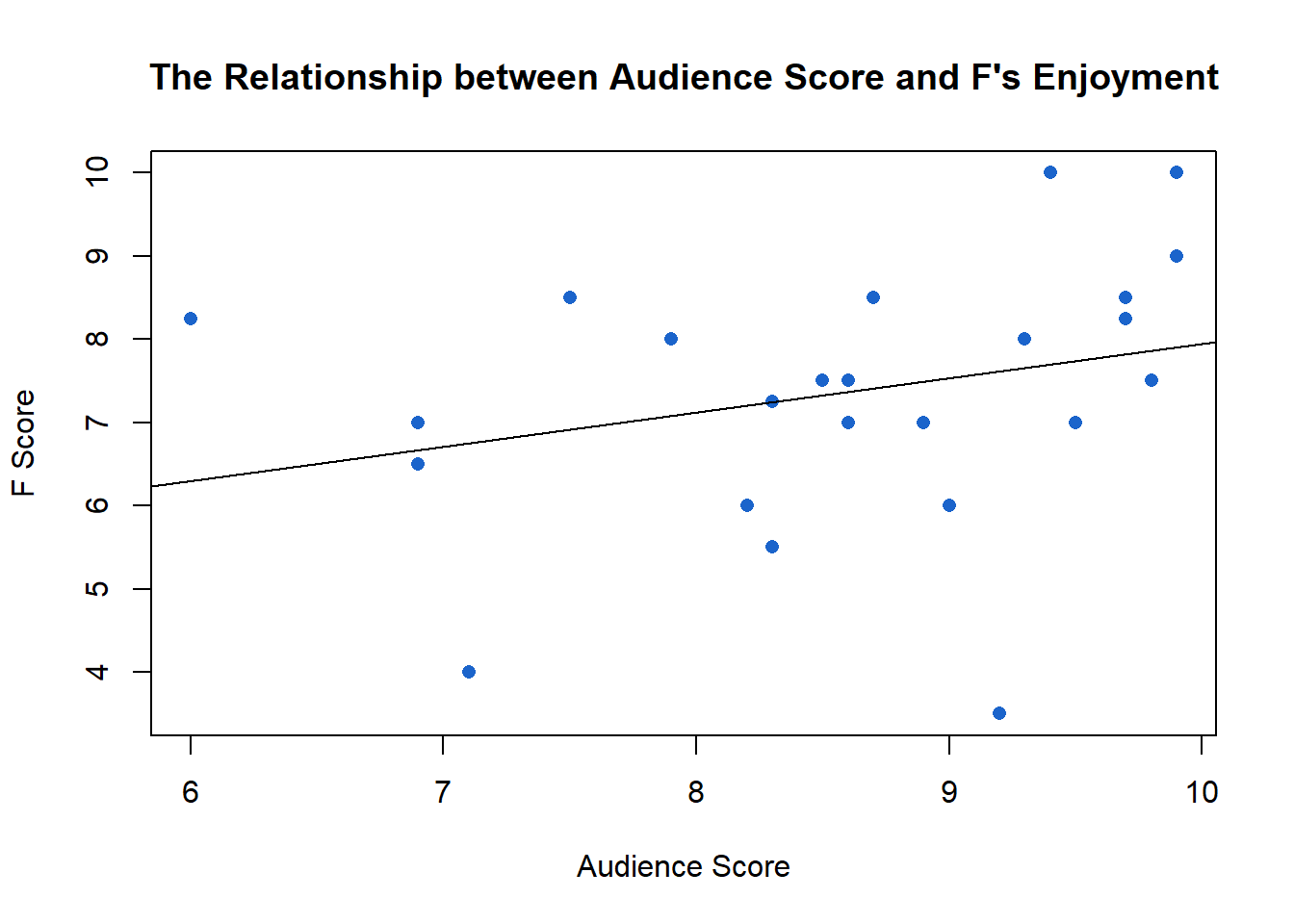
The effect size of audience score on F’s enjoyment is larger than the critics’ score, although the relationship slightly weaker.⁵ A one unit increase in audience score is associated with a 0.41 change in F’s enjoyment.

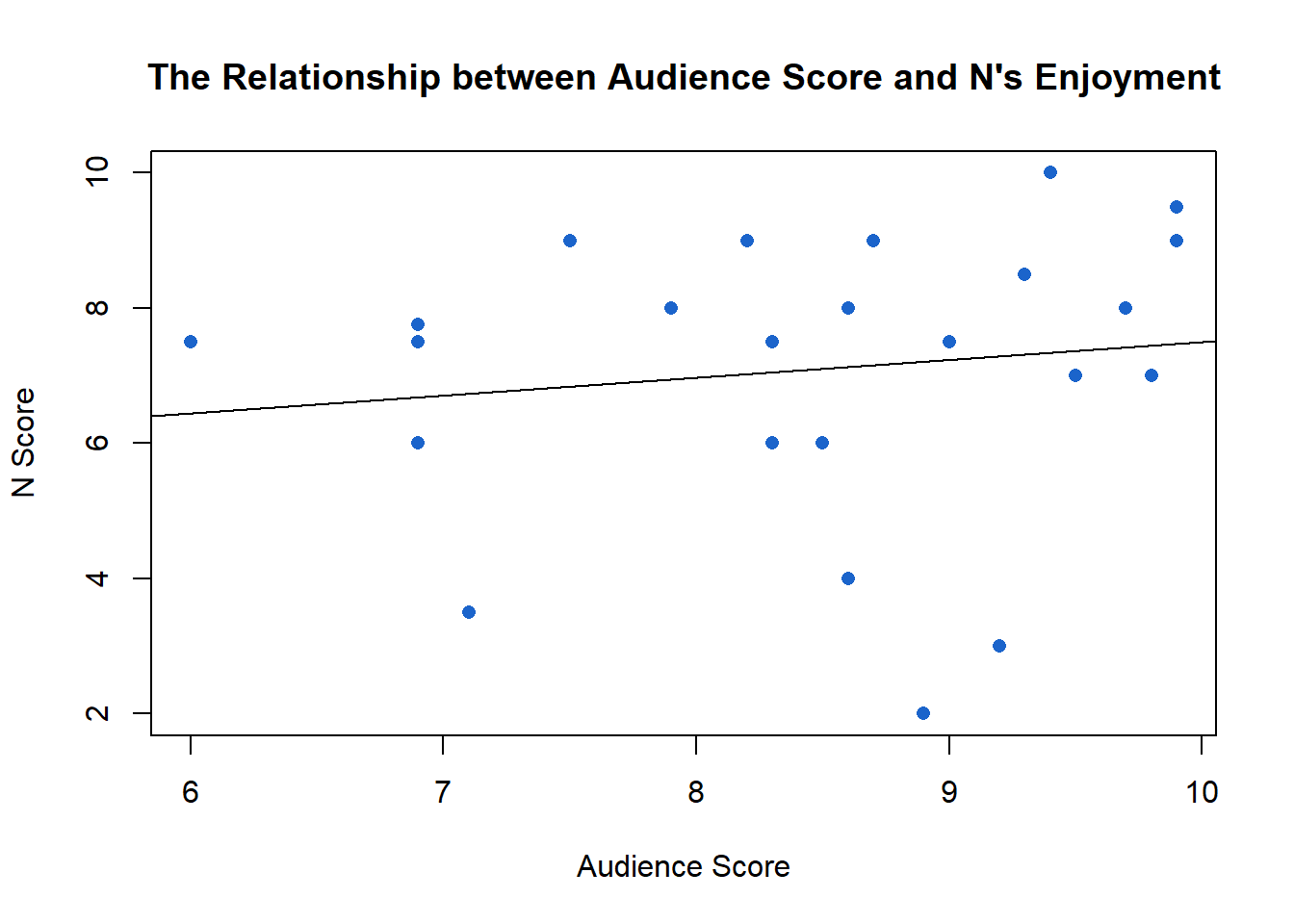
Once again, N’s enjoyment looks to be less related to outside scores.⁶ A one unit change in audience score is associated with only a 0.26 increase in her enjoyment scores.

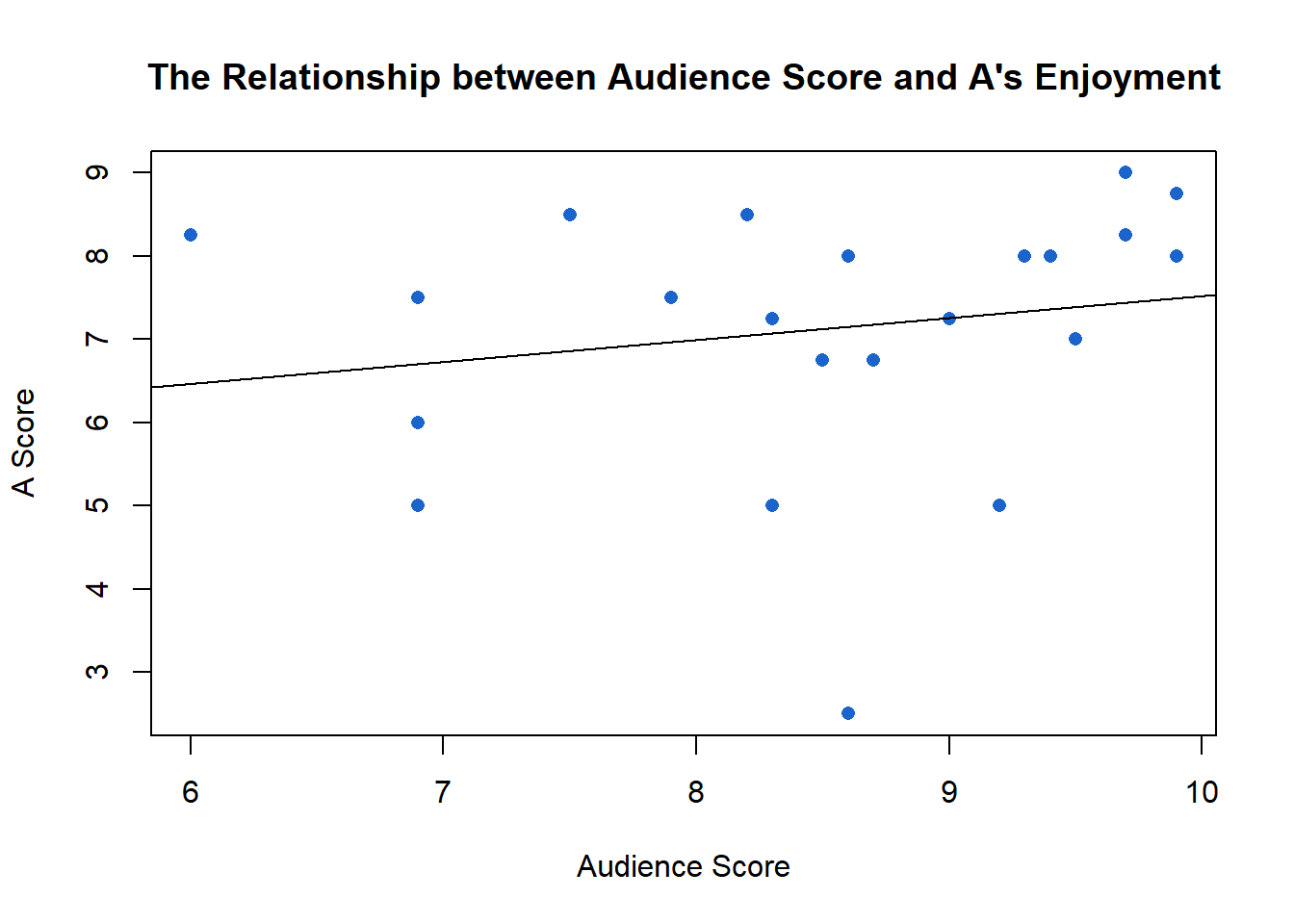
A’s enjoyment scores have a similarly weak relationship with audience scores.⁷ A one unit change in audience scores is associated with a 0.27 change in enjoyment scores.

So far, neither Rotten Tomato critic scores or audience scores seem to matter for these roommates. So what can we find that does better predict how much they will enjoy a certain movie? One answer may be each other.

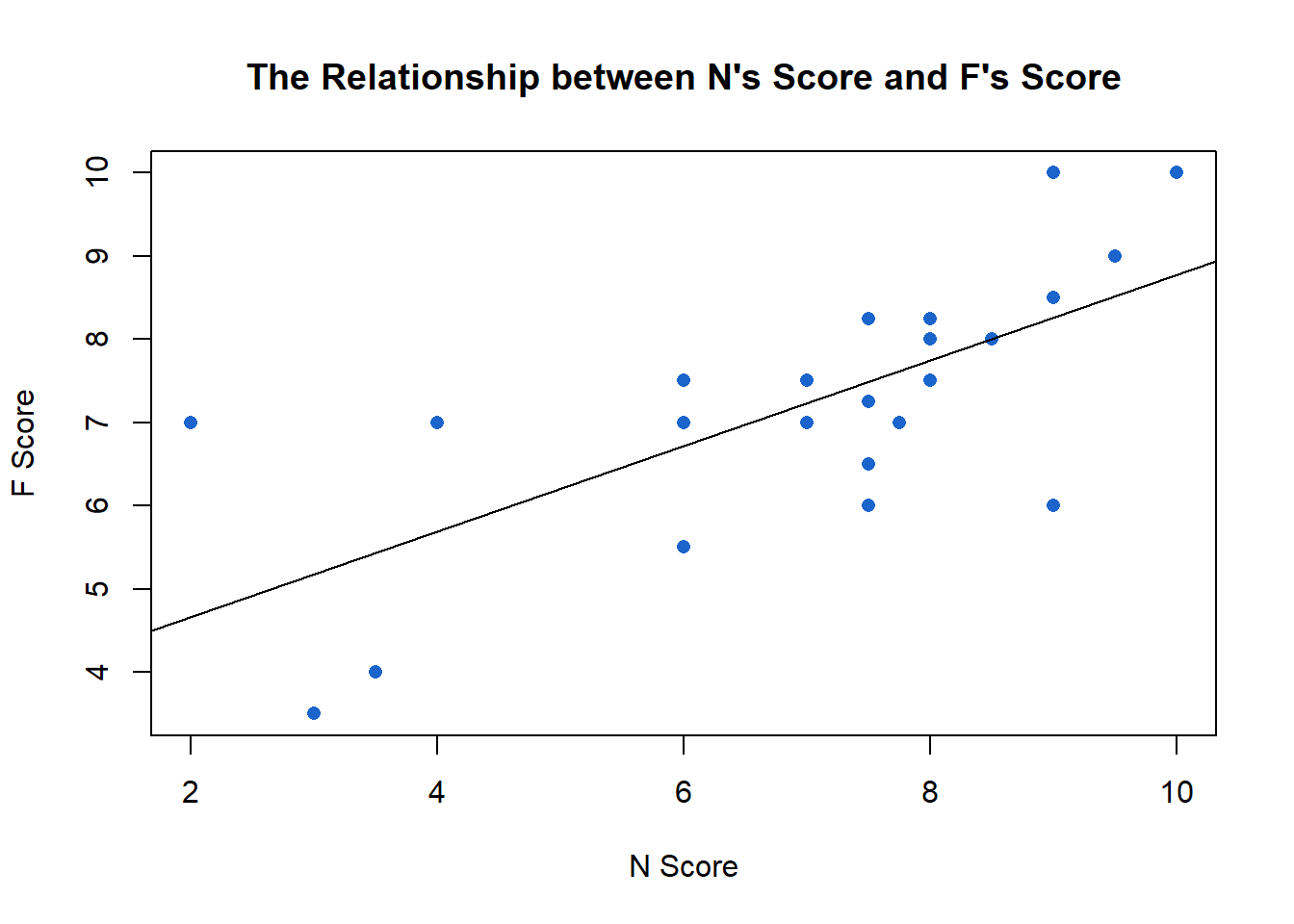
The above graph shows the relationship between movies F watches and N watches. They are highly correlated.⁸ Any movie that N likes, F will generally like too. If N scores a movie an extra point, F will score it an extra half a point. Thinking about predicted variation, whether N says she likes a movie explains about half the variation in F’s scores.⁹

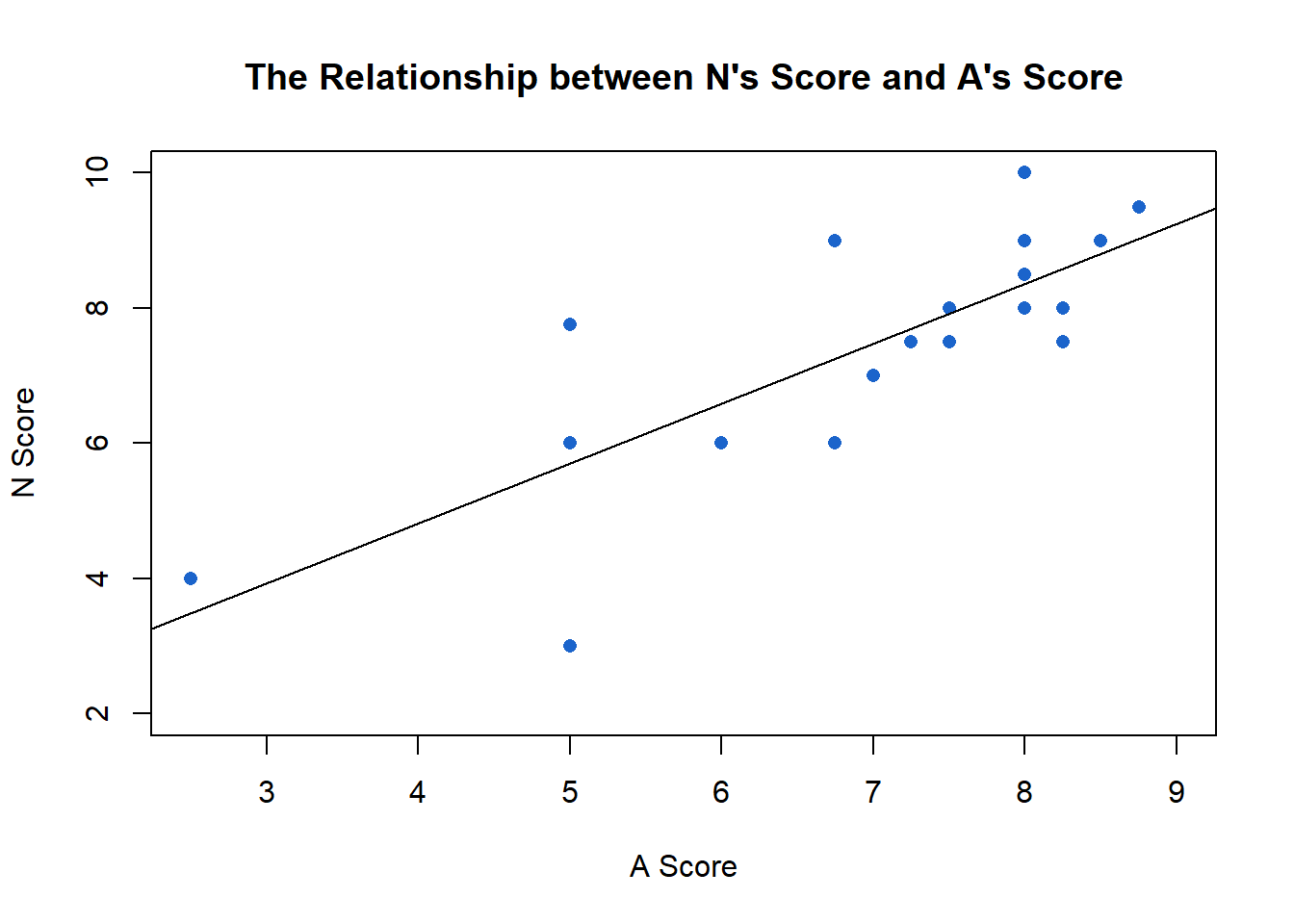
N and A are even more similar.¹⁰ In fact this is the strongest statistical relationship of all. A’s enjoyment of a movie explains 63% of the variation of why N likes a movie. When A bumps a movie rating up one point, N will bump it up 0.89 points; i.e. their scores essentially move in lock step. You can see that clearly in the scatter plot; movies A likes are nearly always the movies N likes. And the observations (the individual movies) are clustered close to the regression line (where they are predicted to fall).

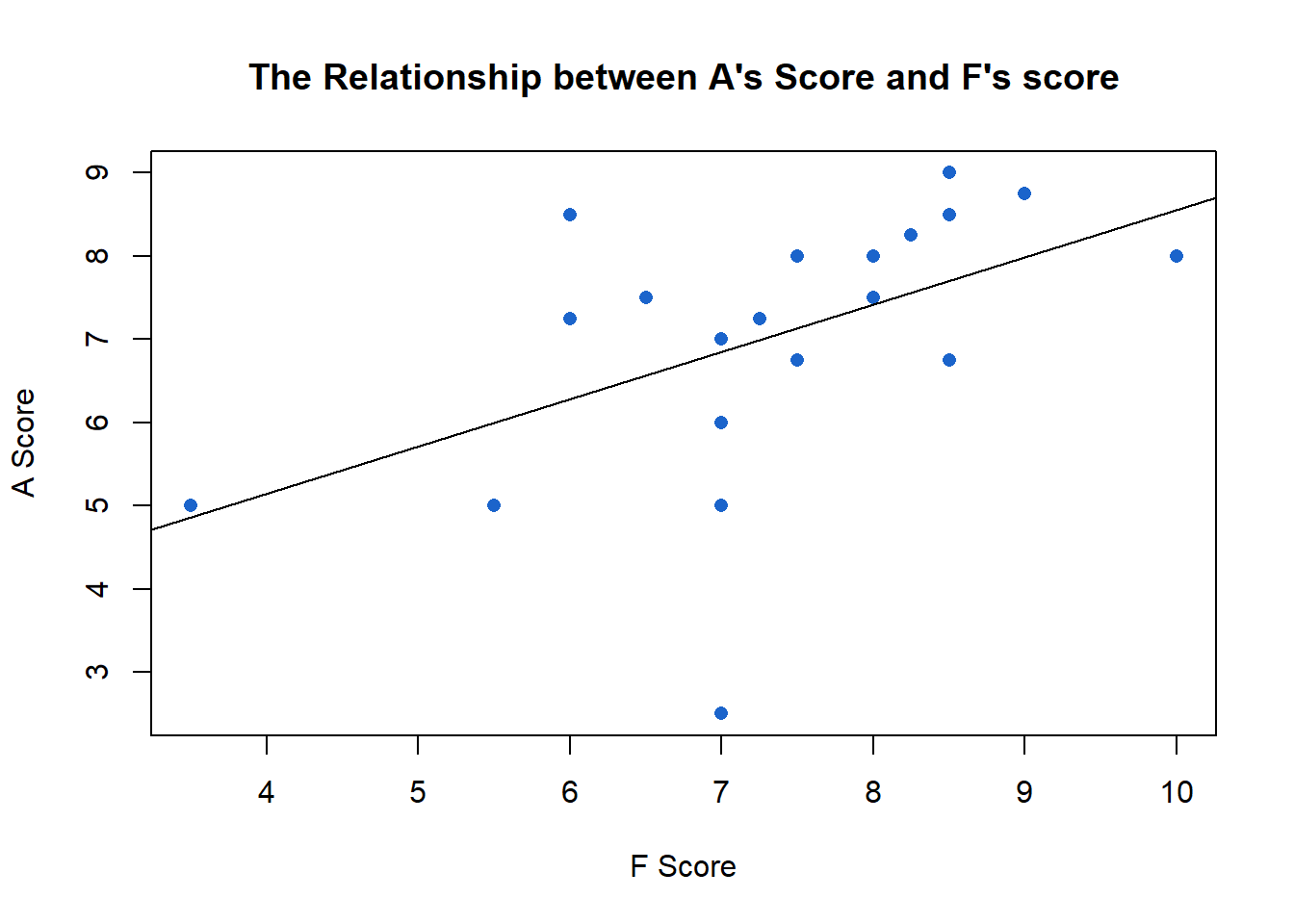
F and A’s scores are also highly correlated, though not at quite the same rate as A and N.¹¹ When F nudges a movie up the scale 1 point, that is associated with a 0.57 increase in A’s score.